Explorando el sistema de los números reales.

Sistema de los números reales.

En el conjunto de números reales se incluyen tanto los números racionales como los irracionales. Según la convención, se utiliza una línea infinitamente extensa para representar los números reales, con los positivos ubicados a la derecha del 0 y los negativos a la izquierda. Es relevante destacar que en cada punto de la recta numérica, hay un número real correspondiente, y viceversa; es decir, para cada número real, existe un punto correspondiente en la recta que lo representa.

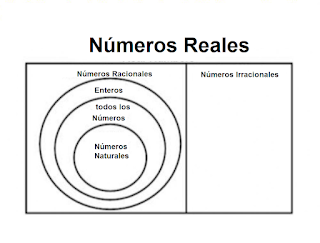
En la representación gráfica del sistema de números reales, como se ilustra en la segunda figura, se evidencia una estructura dividida en dos conjuntos fundamentales: los números racionales y los números irracionales. Dentro de los números racionales, se identifican subconjuntos que incluyen los números naturales (1, 2, 3, ...), los números enteros (0, 1, 2, 3, ...) y los números enteros negativos (0, -1, -2, -3, ...). La figura destaca claramente que el conjunto de números naturales es un subconjunto del conjunto de números enteros, y a su vez, el conjunto de números enteros es un subconjunto del conjunto de números racionales.

Este análisis visual nos proporciona una comprensión clara de la jerarquía y las relaciones entre los distintos conjuntos dentro del sistema de números reales, facilitando la interpretación de su estructura matemática.

Propiedades de los números reales.

También hemos explorado las diversas características de los números reales. En nuestras conversaciones, abordaremos la naturaleza de los números reales, considerando sus distintas propiedades.

 

(1)          conmutativo 

Conmutativo tanto en la adición como en la multiplicación; en otras palabras, para cualquier par de números reales a y b, se cumple que

a + b = b + a               y         

ab = ba.

 

(2)   asociativo 

Asociativo tanto en la adición como en la multiplicación; es decir, para cualquier conjunto de números reales a, b y c.

 ( a + b ) + c =  a  + ( b + c ).

 

(3)   distributivo 

Distributivo en relación con la adición. En otras palabras, para cualquier conjunto de números reales a, b y c.

   a ( b + c ) = ab + ac. 

 

Ahora nos adentramos en propiedades adicionales que aún no han sido abordadas. Examinamos la presencia de elementos identidad y las inversas tanto a la operación de suma como a la de multiplicación.

 

(4)   identidad 

Identidad en la operación de suma y multiplicación. En el caso de la suma, para cada número real a, existe un número 0 tal que

a + 0 = a  = 0 + a ; 

En el contexto de la multiplicación, para cada número real a, existe un número 1 que cumple con la condición de.

a (1) = a = (1 ) ( a )

 

(5)   inversas . Para cualquier número real a, existe un inverso aditivo –a, cumpliendo así que a + – a = 0 = – a + a ; para todos los números reales a, existe un inverso multiplicativo 1/ a tal que a (1/ a ) = 1 = (1/ a )( a )

 

Es importante destacar la conversación acerca de la clausura de los números reales. Esto implica que al realizar operaciones como suma, resta o multiplicación entre números reales, el resultado continúa siendo un número real. No obstante, la división de números reales no sigue esta regla de clausura, ya que no podemos dividir ningún número real entre 0.

 

En conclusión, Los números reales, abarcando racionales e irracionales, son fundamentales y versátiles en matemáticas. Su estructura, con propiedades notables y excepciones como la división por cero, provee un sólido marco para entender fenómenos en ciencias aplicadas, destacando su esencial papel en el análisis matemático.